Rugby World Cup 2023 megastore opens its doors in the heart of Paris as excitement builds up in the host country | Rugby World Cup 2023

Coupe du monde féminine de football : à la boutique de la FFF à Paris, ces clients sont venus pour les Bleues - Le Parisien

Le maillot de Mbappé au PSG "disparaît" de la boutique officielle des fans au milieu des rumeurs avec le Real Madrid - Football | Tribuna.com

2 joueurs dont les maillots se vendent comme des petits pains au Real Madrid - Football | Tribuna.com

La Boutique officielle du Puy du Fou - Coffrets cadeaux, costumes, jeux et jouets - Boutique Puy du Fou
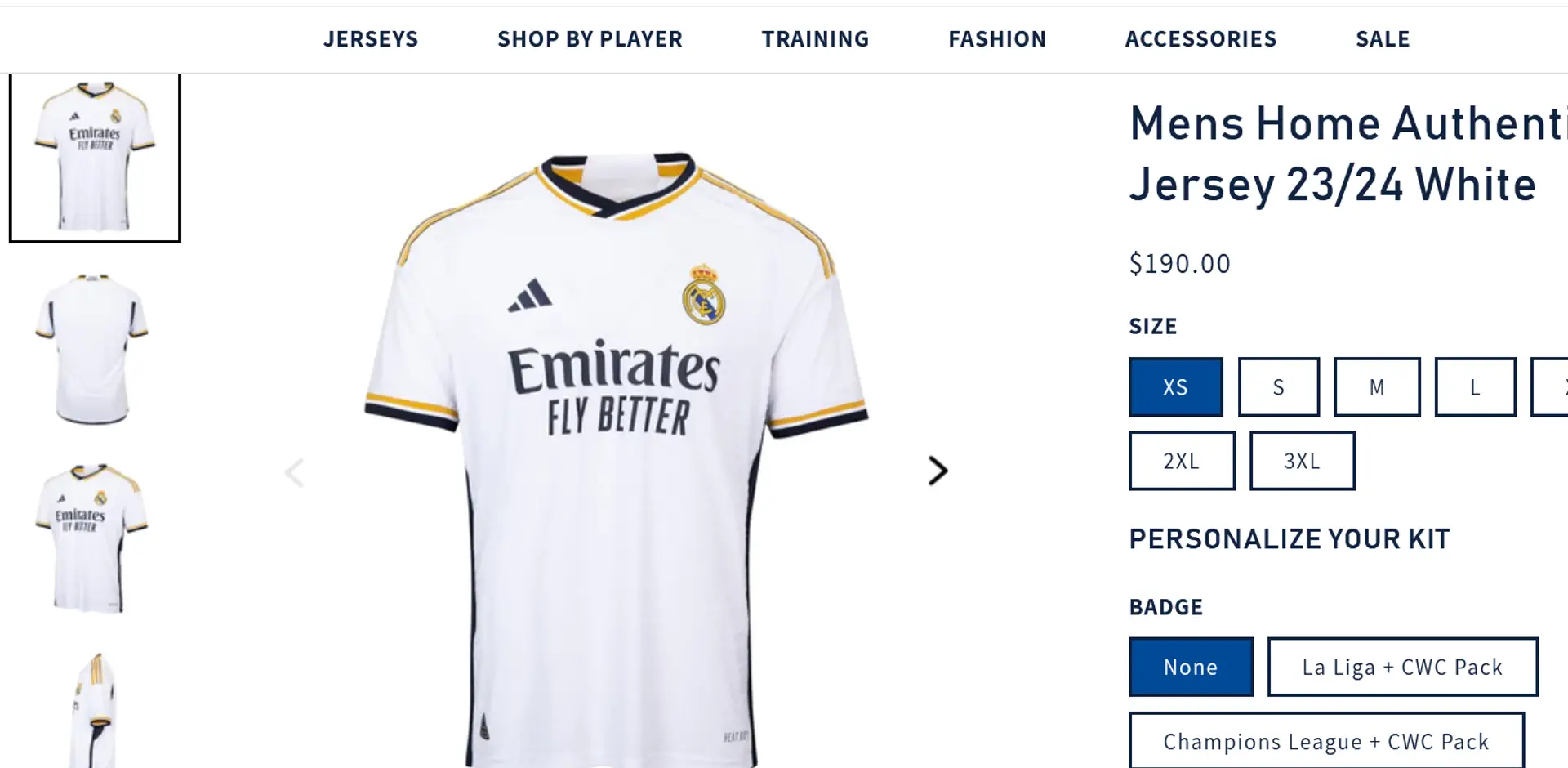
2 joueurs dont les maillots se vendent comme des petits pains au Real Madrid - Football | Tribuna.com

Vente privée abonnés à la Boutique Officielle | Football Club de Metz - Infos FC Metz - Entraînements FC Metz - Vidéos FC Metz

La Boutique officielle du Puy du Fou - Coffrets cadeaux, costumes, jeux et jouets - Boutique Puy du Fou








:focal(545x417.5:555x407.5)/cloudfront-eu-central-1.images.arcpublishing.com/ipmgroup/6CEOJSVVHBCXNE624ZTE3QKYYI.jpg)